Les angles, leurs diverses unités, leurs valeurs remarquables, les propriétés qui en découlent, l’aire d’un disque, tout ceci est nécessaire pour étudier les triangles et la trigonométrie.
Définition
La trigonométrie
Une première vidéo est consacrée au lien entre les lignes trigonométriques et le théorème de Thalès (il faut bien que ce théorème serve une fois dans le cursus scolaire!), et les valeurs concernant les angles remarquables:
Le cercle trigonométrique, sa définition, ses propriétés:
Construire en moins d’une minute le cercle trigonométrique pour lire les cosinus, sinus et tangentes des angles remarquables.
Définition d’une fonction
Qu’est-ce qu’une fonction?
Qu’est-ce qu’un ensemble de définition d’une fonction?
Pourquoi il ne faut pas confondre une courbe et une fonction?
Quelles sont les premières fonctions de référence et leur domaine de définition?
Toutes ces questions sont légitimes, et il est souhaitable de maîtriser le vocabulaire qui permet d’y répondre.
Les vecteurs
Les vecteurs sont des outils mathématiques indispensables en physique, et font l’objet d’une généralisation très importante en algèbre.
La première partie de ce chapitre est accessible à partir de la fin du collège et approfondit des notions abordées en début de lycée.
On y définit un vecteur comme une flèche, on définit l’addition des vecteurs et la colinéarité; au passage on présente la valeur absolue; on y montre ce qu’est la projection d’un vecteur.
La deuxième partie traite des composantes d’un vecteur et des coordonnées d’un point dans un repère orthonormé.
La troisième partie donne des démonstrations de la distance entre 2 points, des coordonnées du milieu d’un segment, et des diverses expressions de la colinéarité dans un repère orthonormé de dimension 2.
La fonction dérivée: définition
La fonction f’, dérivée d’une fonction f, appliquée à un réel x appartenant au domaine de dérivabilité de la fonction f, donne la valeur du coefficient directeur de la tangente à la courbe représentative de f, au point d’abscisse x.
Vidéo en préparation
Les équations
Une équation est une égalité comportant une ou plusieurs inconnues.
Résoudre une équation, c’est faire les calculs qui permettent de trouver la valeur ou l’expression des inconnues.
Une équation différentielle est une équation pour laquelle l’inconnue est une fonction qui intervient avec ses dérivées.
Vidéo en préparation
Exemples de vecteurs
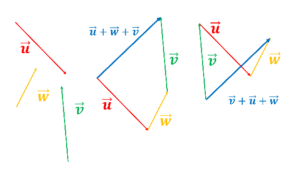
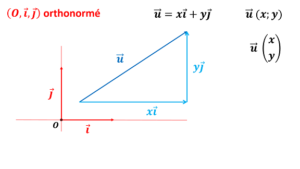
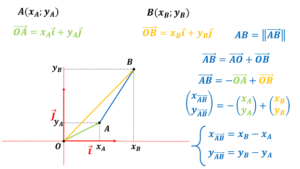
Un vecteur est une représentation d’une grandeur physique orientée dans l’espace, en translation ou en rotation.
- Un vecteur peut représenter un poids, pas une masse;
- Un vecteur peut représenter une force, pas une pression, ni une température;
- Un vecteur peut représenter une vitesse, une accélération;
- Un vecteur peut représenter une surface, mais pas un volume.
- Un vecteur peut représenter une vitesse, une accélération;
- Un vecteur peut représenter une vitesse angulaire, une accélération angulaire, un moment;
- Un vecteur peut représenter un champ magnétique, mais pas un flux magnétique.
Les puissances de 10
Les puissances de 10 sont des outils mathématiques absolument indispensables en physique, par exemple pour des conversions d’unités de mesure; on les introduit dès la fin du primaire, et leur construction, leurs propriétés et leur utilisation se consolident au fil des années.
En vidéo, il sera plus facile de comprendre la construction des puissances de 10, pour mémoriser simplement des résultats très importants, et pas forcément intuitifs.
Les règles de calculs des puissances de 10 sont, bien sûr, issues des règles de calcul des puissances d’un nombre quelconque. Trois vidéos vous permettront de comprendre ces règles élémentaires, apprendre à les manipuler et bien les retenir.