Les angles, leurs diverses unités, leurs valeurs remarquables, les propriétés qui en découlent, l’aire d’un disque, tout ceci est nécessaire pour étudier les triangles et la trigonométrie.
Lycée
La trigonométrie
Une première vidéo est consacrée au lien entre les lignes trigonométriques et le théorème de Thalès (il faut bien que ce théorème serve une fois dans le cursus scolaire!), et les valeurs concernant les angles remarquables:
Le cercle trigonométrique, sa définition, ses propriétés:
Construire en moins d’une minute le cercle trigonométrique pour lire les cosinus, sinus et tangentes des angles remarquables.
Définition d’une fonction
Qu’est-ce qu’une fonction?
Qu’est-ce qu’un ensemble de définition d’une fonction?
Pourquoi il ne faut pas confondre une courbe et une fonction?
Quelles sont les premières fonctions de référence et leur domaine de définition?
Toutes ces questions sont légitimes, et il est souhaitable de maîtriser le vocabulaire qui permet d’y répondre.
Les paraboles
Les paraboles représentent les fonctions polynomiales du second degré;
la première partie du chapitre est actuellement effleuré en milieu de la classe de seconde, il s’agit de la forme canonique d’un trinôme du second degré;
les explications s’appuient sur les chapitres
la deuxième partie est abordée au tout début de la classe de première, il s’agit de la factorisations des trinômes du second degré et des équations du second degré;
Les fonctions polynomiales
C’est un chapitre qui ne fait pas explicitement partie du programme au lycée, mais il faut s’y référer souvent, sans le dire….. Bref, tout ira mieux en le disant!!!
Il permettra de mieux comprendre tout ce qui concerne les équations du second degré, entre autres choses.
Les vecteurs
Les vecteurs sont des outils mathématiques indispensables en physique, et font l’objet d’une généralisation très importante en algèbre.
La première partie de ce chapitre est accessible à partir de la fin du collège et approfondit des notions abordées en début de lycée.
On y définit un vecteur comme une flèche, on définit l’addition des vecteurs et la colinéarité; au passage on présente la valeur absolue; on y montre ce qu’est la projection d’un vecteur.
La deuxième partie traite des composantes d’un vecteur et des coordonnées d’un point dans un repère orthonormé.
La troisième partie donne des démonstrations de la distance entre 2 points, des coordonnées du milieu d’un segment, et des diverses expressions de la colinéarité dans un repère orthonormé de dimension 2.
L’équation d’une droite
Suite aux différents décalages de la droite de référence, on obtient une droite quelconque d’équation y=ax+b ou encore kx+cy+d=0;
Dans une première partie, on précise ce qu’est une équation, une équation réduite, une équation cartésienne, et la pente de la droite.
Dans une deuxième partie, on détermine l’équation à partir de 2 données : les coordonnées d’1 point et le coefficient directeur.
Pour obtenir le coefficient directeur,
- soit il est directement donné,
- soit on a les coordonnées d’un deuxième point
- soit on a les coordonnées d’un vecteur directeur,
- soit on peut calculer le nombre dérivé f′(x_A) d’une fonction f en l’abscisse x_A d’un point A. On pourra alors déterminer l’équation de la tangente à la courbe représentant f, au point A.
Les probabilités conditionnelles
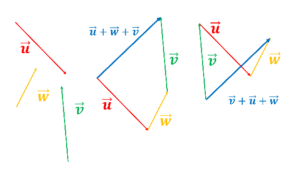
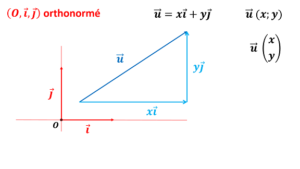
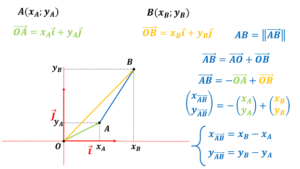
L’objet de cette leçon est
- de présenter séparément
- le vocabulaire et les formules de la théorie des ensembles,
- du vocabulaire et des formules utilisés en probabilité, qui s’appuient sur les précédents
- de présenter les probabilités conditionnelles à l’aide de dessins de type « patates » utilisés pour les ensembles.
La droite de référence
Les droites…… vaste programme; il existe de nombreuses façons de présenter les propriétés des droites, leurs constructions, leurs équations. Je vous donne dans ces vidéos, quelques approches différentes du programme officiel, pour faire le lien avec certains chapitres abordés au lycée, voire après le BAC.
Ensuite, on peut calculer les paramètres de l’équation d’une droite à partir de quelques informations, et la représenter.
Vidéos sur les pourcentages, les paraboles, les fonctions trigonométriques, les exponentielles et les logarithmes, en préparation.
Les décalages canoniques des fonctions
Quelle est l’expression analytique des fonctions représentées par ces différentes courbes?
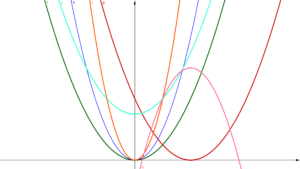
Il existe un lien étroit entre toutes; une fois que ce raisonnement est bien compris, les portes s’ouvrent!
Les explications à partir d’une fonction quelconque seront précieuses pour les applications aux fonctions de référence.